本文是全系列中第1 / 5篇:高频交易策略的思考
- 高频交易策略的思考(五)
- 高频交易策略的思考(四)
- 高频交易策略的思考(三)
- 高频交易策略的思考(二)
- 高频交易策略的思考(一)
转载自http://FMZ.COM,作者:小草
上篇文章初步介绍了各种中间价的计算方法,并给出了一种中间价的修订,本文继续深入这个话题。
所需数据
订单流数据和十档的深度数据,来自于实盘收集,更新频率都是100ms。实盘的只包含买一卖一盘口数据是实时更新的,为了简洁,暂时不用。考虑到数据太大,只保留了10万行深度数据,并且把逐档行情也独立为单独的列。
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inlinetick_size = 0.0001trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
'transact_time', 'is_buyer_maker'])trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
'transact_time':'last',
'agg_trade_id': 'last',
'price': 'first',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
})trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])depths = depths.iloc[:100000]depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()def expand_bid(bid_data):
expanded = {}
for j, (price, quantity) in enumerate(bid_data):
expanded[f'bid_{j}_price'] = float(price)
expanded[f'bid_{j}_quantity'] = float(quantity)
return pd.Series(expanded)
def expand_ask(ask_data):
expanded = {}
for j, (price, quantity) in enumerate(ask_data):
expanded[f'ask_{j}_price'] = float(price)
expanded[f'ask_{j}_quantity'] = float(quantity)
return pd.Series(expanded)
# 应用到每一行,得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);trades = trades[trades['transact_time'] 先看下这20档档行情的分布,符合预期,距离盘口越远,一般挂单也多,且买单挂单和卖单挂单大致对称。
bid_mean_list = []
ask_mean_list = []
for i in range(20):
bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)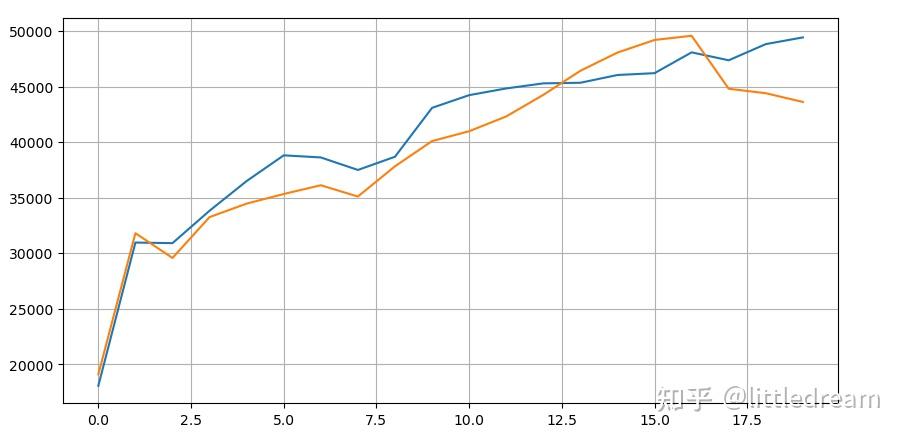
把深度数据和成交数据进行合并,方便评估预测的准确性。这里保证成交数据都是晚于深度数据,在不考虑延时的情况下,直接计算预测值与实际成交价的均方误差。用于衡量预测的准确度。
从结果来看,买一卖一平均值mid_price的误差最大,改为weight_mid_price后,误差立刻小了很多,用调整加权中间价又改进了一点。昨天的文章发出后,有人反馈只用I^3/2,这里检查了下,发现结果更好了。思考了下原因,应该是事件发生频率的不同,I在接近-1和1时是低概率事件,为了修正这些低概率,反而把高频率发生的事件预测的不那么精确了,因此,在更照顾高频率事件的情况下,我又调整了下(这里是纯粹的试出来的参数,实盘参考意义不大):
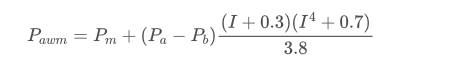
结果又稍好了一些。上篇文章说过,策略应该用跟多的数据来预测,在有了更多深度和订单成交数据的情况下,纠结与盘口能获得的提升已经很弱了。
df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8print('平均值 mid_price的误差:', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差:', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的 mid_price的误差:', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差:', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差:', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差:', ((df['price']-df['adjust_mid_price_4'])**2).sum())平均值 mid_price的误差: 0.0048751924999999845
挂单量加权 mid_price的误差: 0.0048373440193987035
调整后的 mid_price的误差: 0.004803654771638586
调整后的 mid_price_2的误差: 0.004808216498329721
调整后的 mid_price_3的误差: 0.004794984755260528
调整后的 mid_price_4的误差: 0.0047909595497071375考虑第二档深度
这里用上一篇的思路,考察某个影响参数的的不同取值范围,成交价的变化来衡量这个参数对中间价的贡献。如第一档深度的图,随着I的增加,成交价接下来成交价越可能正向变化,这说明I做了正的贡献。
第二档用同样的方式处理,发现虽然效应比第一档小了一些,但任然不容忽略。第三档深度也有微弱的贡献,但单调性差了很多,更深的深度基本没有参考价值了。
根据贡献程度不同,这三档的不平衡参数,分配了不同的权重,实际检查对于不同的计算方式,预测误差都进一步下降。
bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))
axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)
axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)
axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)
axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();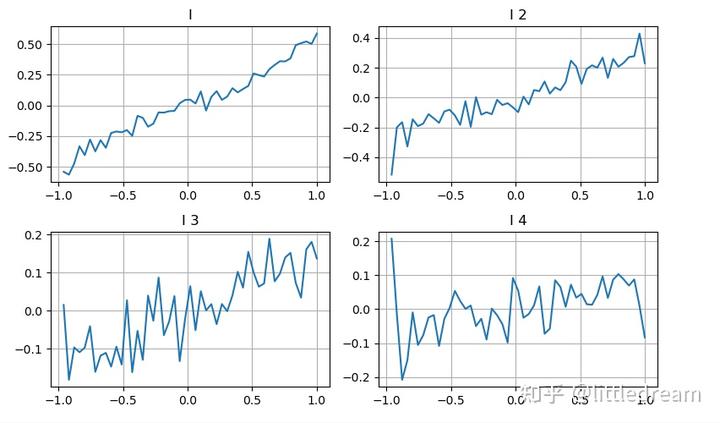
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8print('调整后的 mid_price_4的误差:', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差:', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差:', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差:', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差:', ((df['price']-df['adjust_mid_price_8'])**2).sum())调整后的 mid_price_4的误差: 0.0047909595497071375
调整后的 mid_price_5的误差: 0.0047884350488318714
调整后的 mid_price_6的误差: 0.0047778319053133735
调整后的 mid_price_7的误差: 0.004773578540592192
调整后的 mid_price_8的误差: 0.004771415189297518考虑成交数据
成交数据直接反映了多空的程度,毕竟这是真金白银参与的选择,而挂单的成本低很多,甚至还有故意挂单欺骗的情况。因此预测中间价,策略要重点考虑成交数据。
考虑到形式,定义订单平均到达数量不平衡VI,Vb,Vs分别表示买单和卖单的单位事件内平均数量。
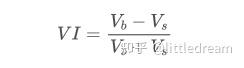
结果发现短时间内的到达数量对价格变化预测最为显著,当VI处于(0.1-0.9)之间时,与价格负相关,而在区间之外反而与价格迅速的正相关。这提示着,当行情不极端时,以震荡为主,价格会均值回归,当极端行情出现时,如大量的买单压过卖单,此时会走出趋势。即使不考虑这些低概率情况,简单假设趋势和VI满足负的线性关系,对中间价的预测误差又大幅下降。式子中的a代表系数。
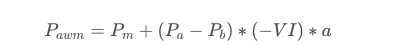
alpha=0.1df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')
df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']
df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)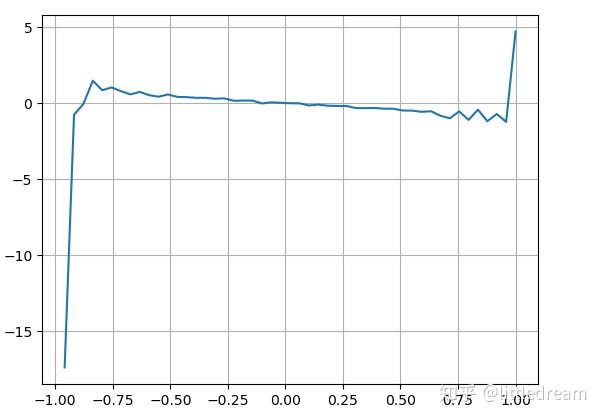
df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4print('调整后的mid_price 的误差:', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差:', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差:', ((df['price']-df['adjust_mid_price_10'])**2).sum())调整后的mid_price 的误差: 0.0048373440193987035
调整后的mid_price_9 的误差: 0.004629586542840461
调整后的mid_price_10的误差: 0.004401790287167206综合的中间价
考虑到挂单量和成交数据都对中间价的预测有帮助,因此可以把这两个参数合并在一起,这里权重的赋值比较随意,也没有考虑边界的条件,极端情况下,预测的中间价可能不在买一和卖一之间,但只要误差能够减小,也不在意这些细节了。
最后预测的误差从最开始的0.00487降到了0.0043,到这里就不继续深入了,中间价可挖掘的内容还有很多,毕竟预测中间价就是在预测价格,大家可以自己尝试。
#注意VI需要延后一个使用
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差:', ((df['price']-df['adjust_mid_price_11'])**2).sum())调整后的mid_price_11的误差: 0.0043001941412563575总结
本文结合深度数据和成交数据,进一步改进了中间价的计算方法,本给出了衡量准确性的方法,提高了对价格变化预测的准确性。整体上各种参数都不太严谨,仅供参考。有了较为精确的中间价,接下来就是实际应用中间价进行回测了,这一部分内容也很多,先暂停一段时间更新。
文章来源于互联网:高频交易策略的思考(五)
本文是全系列中第1 / 5篇:高频交易策略的思考
- 高频交易策略的思考(五)
- 高频交易策略的思考(四)
- 高频交易策略的思考(三)
- 高频交易策略的思考(二)
- 高频交易策略的思考(一)


